2012年1月27日星期五
在 Altium designer 09 中显示/隐藏飞线 可指定飞线
一种是在PCB编辑界面按“N”,弹出的菜单中选show Connections,再选“All” 即可 。(这个简单)
还有一种是在PCB编辑界面按“L”弹出“Board Layers And Colors”配置对话框,再将“Default Color For New Nets”勾选上,若已经勾上或没有作用可多设置几次,就好了。
画PCB技巧:在PCB设计中鼠标指针一般有栅格捕获效果,可以把鼠标指针自动对齐到栅格位置上,对元器件的对齐和画线的美观很有帮助。但是这种功能并不总是有用,要临时关闭捕获功能,只要按住CTRL键就可以了。
Photoshop制作磨砂玻璃的文字说明
本教程主要使用Photoshop制作磨砂玻璃的文字说明,在这个快速的教程里,我们将会展示如何创建类似于磨砂玻璃的文字说明来提高你的图片或者设计的外观。下面让我们一起来学习。
来源:飞鱼的声纳
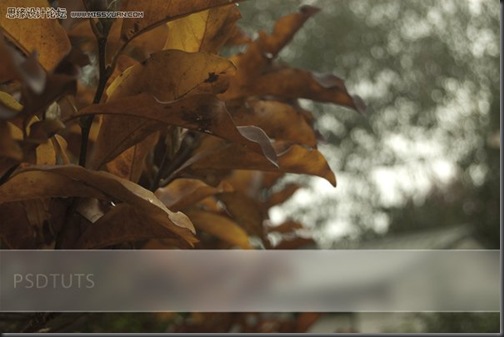
最终效果:
第一步
在Photoshop中打开一张图片。我使用了一张秋天的图片。你可以使用一张你喜欢的类似的图片。或者,任何图片都行。在背景图层上双击对背景层解除锁定,将其命名为”Leaves”。
第二步
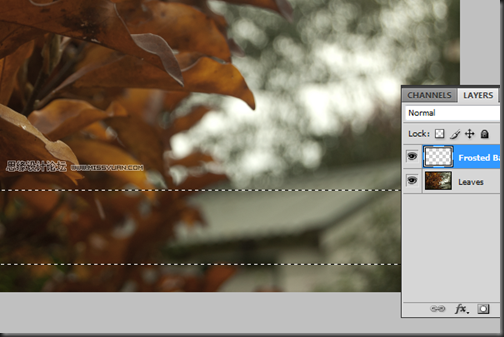
在树叶的图层上方创建一个新图层(Ctrl+N),命名为”Frosted Bar”。选择”Frosted Bar”图层,使用矩形选区工具(M)拖出一个选区,确保选区的两边一直要触及到图片的两边。选区的位置取决于你,在这个例子中我将它放置在了图片的底部,如下图所示:
第三步
使用油漆桶工具(G)将选区填充为白色(#FFFFFF),取消选区。(Ctrl+D)
第四步
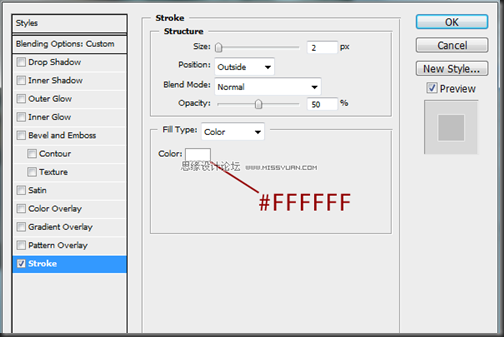
给”Frosted Bar”图层应用如下图层样式:(混合选项:自定义–在高级混合选项中将填充不透明度设置为20%)
描边:使用白色(#FFFFFF),大小为2个像素,位置为外部,不透明度为50%。
第五步
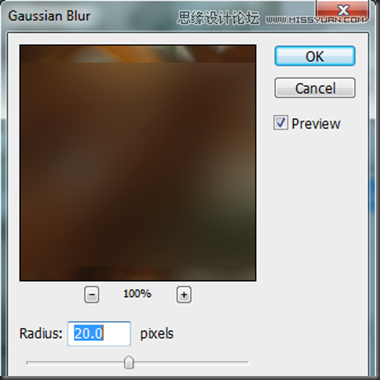
我们将要编辑我们原始的图片,因此我们最好将它复制一遍,这样我们可以随时撤销编辑。因此选择树叶图层复制(Ctrl+J)。选择复制好的树叶图层,按住Ctrl键,在图层面板中点击”Frosted Bar”图层图标选取选区。应用高斯模糊(滤镜>模糊>高斯模糊),半径设置为20点击确定。
第六步
基础的毛玻璃效果已经做好了,接下来我们应用高光。在毛玻璃横条图层的上方创建一个新的图层(Ctrl+Shift+N),命名为”Highlights”。再次载入毛玻璃条的选区,选择画笔工具(B)。使用大一些的柔软的画笔(500像素,没有硬度,颜色为白色#FFFFFF)在横条的中间部分上下都画出高光(如下图),最后将图层的不透明度更改为60%。
第七步
最后一步是添加文字。使用文字工具(T)在横条中间添加你想要的文字,选择合适的文字大小(在这个例子中文字大小为100像素)。将文字图层的不透明度降低为40%,图层混合模式更改为叠加,完成。
最终效果
希望你能喜欢这个教程!
2012年1月25日星期三
关于没root的recovery后卡在红三角的退出方法
那就是..........................(音量加+开机键)(想不到啊想不到!),希望这个帖子对和我一样的小白有帮助,大家过年好~!
2012年1月24日星期二
Android获得Root权限后文件系统仍然报Read-Only的问题
例如系统报:rm failed for xxx.apk, Read-only file system
只要执行命令:mount -o rw,remount -t yaffs2 /dev/block/mtdblock3 /system 即可。
2012年1月23日星期一
2012年1月6日星期五
28个不得不看的经典编程算法!!
发起人的描述:《来自圣经的证明》收集了数十个简洁而优雅的数学证明,迅速赢得了大批数学爱好者的追捧。如果还有一本《来自圣经的算法》,哪些算法会列入其中呢?
第一名:Union-find
严格地说,并查集是一种数据结构,它专门用来处理集合的合并操作和查询操作。并查集巧妙地借用了树结构,使得编程复杂度降低到了令人难以置信的地步;用上一些递归技巧后,各种操作几乎都能用两行代码搞定。而路径压缩的好主意,更是整个数据结构的画龙点睛之笔。并查集的效率极高,单次操作的时间复杂度几乎可以看作是常数级别;但由于数据结构的实际行为难以预测,精确的时间复杂度分析需要用到不少高深的技巧。
第二名:Knuth-Morris-Pratt字符串匹配算法
关于此算法的介绍,请参考此文:六、教你从头到尾彻底理解KMP算法。KMP算法曾经落选于二十世纪最伟大的十大算法,但人们显然不能接受,如此漂亮、高效的KMP算法竟然会落选。所以,此次最终投票产出生,KMP算法排到了第二名。
第三名:BFPRT 算法
1973 年,Blum、Floyd、Pratt、Rivest、Tarjan集体出动,合写了一篇题为 “Time bounds for selection” 的论文,给出了一种在数组中选出第 k 大元素的算法,俗称"中位数之中位数算法"。依靠一种精心设计的 pivot 选取方法,该算法从理论上保证了最坏情形下的线性时间复杂度,打败了平均线性、最坏 O(n^2) 复杂度的传统算法。一群大牛把递归算法的复杂度分析玩弄于骨掌股掌之间,构造出了一个当之无愧的来自圣经的算法。
我在这里简单介绍下在数组中选出第k大元素的时间复杂度为O(N)的算法:
类似快排中的分割算法:
每次分割后都能返回枢纽点在数组中的位置s,然后比较s与k的大小
若大的话,则再次递归划分array[s..n],
小的话,就递归array[left...s-1] //s为中间枢纽点元素。
否则返回array[s],就是partition中返回的值。 //就是要找到这个s。
找到符合要求的s值后,再遍历输出比s小的那一边的元素。
各位可参考在:算法导论上,第九章中,以期望线性时间做选择,一节中,
我找到了这个 寻找数组中第k小的元素的,平均时间复杂度为O(N)的证明:上述程序的期望运行时间,最后证明可得O(n),且假定元素是不同的。
第四名:Quicksort(快速排序)
快速排序算法几乎涵盖了所有经典算法的所有榜单。它曾获选二十世纪最伟大的十大算法(参考这:细数二十世纪最伟大的10大算法)。关于快速排序算法的具体介绍,请参考我写的这篇文章:一之续、快速排序算法的深入分析,及十二、快速排序算法之所有版本的c/c++实现。
第五名:Floyd-Warshall all-pairs最短路径算法
关于此算法的介绍,可参考我写的此文:几个最短路径算法比较(http://blog.csdn.net/v_JULY_v/archive/2011/02/12/6181485.aspx)。
d[]: 二维数组. d[i,j]最小花费、或最短路径的邻边。
for k from 1 to n:
for i from 1 to n:
for j from 1 to n:
d[i,j] = min(d[i,j], d[i,k] + d[k,j])
第六名:Gentry's Fully Homomorphic Encryption Scheme(绅士完全同态加密机制)算法。
此算法很漂亮,它允许第三方执行任意加密数据运算得不到私钥(不是很了解)。
第七名:Depth First Search、Breadth First Search(深度、广度优先搜索)
它们是许多其他算法的基础。关于深度、广度优先搜索算法的具体介绍,请参考此文:教你通透彻底理解:BFS和DFS优先搜索算法。
第八名:Miller-Rabin作的类似的试验测试
这个想法是利用素数的性质(如使用费马大定理)的小概率寻找见证不数素数。如果没有证据是足够的随机检验后发现,这一数字为素数。
第九名:Binary Search (二分查找)
在一个有序的集合中查找元素,可以使用二分查找算法,也叫二分搜索。二分查找算法先比较位于集合中间位置的元素与键的大小,有三种情况(假设集合是从小到大排列的):
1.键小于中间位置的元素,则匹配元素必在左边(如果有的话),于是对左边的区域应用二分搜索。
2.键等于中间位置的元素,所以元素找到。
3.键大于中间位置的元素,则匹配元素必在右边(如果有的话),于是对右边的区域应用二分搜索。
另外,当集合为空,则代表找不到。
第十名:Huffman coding(霍夫曼编码)
霍夫曼编码(Huffman Coding)是一种编码方式,是一种用于无损数据压缩的熵编码(权编码)算法。1952年,David A. Huffman在麻省理工攻读博士时所发明的,并发表于《一种构建极小多余编码的方法》(A Method for the Construction of Minimum-Redundancy Codes)一文。
十一、Cooley-Tukey FFT算法。快速傅里叶变换算法。关于傅里叶变换算法的介绍,请参考此文:十、从头到尾彻底理解傅里叶变换算法、上,及十、从头到尾彻底理解傅里叶变换算法、下。
十二、linear programming,线性规划。
十三、Dijkstra 算法。与上第五一样,又一种最短路径算法。具体介绍,请参考:二之续、彻底理解Dijkstra算法,和二(再续)、Dijkstra 算法+fibonacci堆的逐步c实现。
十四、Merge Sort。归并排序。
十五、Ford–Fulkerson算法。网络最大流算法。
十六、辗转相除法。
在数学中,辗转相除法,又称欧几里得算法,是求最大公约数的算法,即求两个正整数之最大公因子的算法。此算法作为TAOCP第一个算法被阐述,足见此算法被重视的程度。它是已知最古老的算法, 其可追溯至3000年前。辗转相除法首次出现于欧几里得的《几何原本》(第VII卷,命题i和ii)中,而在中国则可以追溯至东汉出现的《九章算术》。扩展的辗转相除法则构造性地证明了,对任意整数a和b ,存在一对x、y使得 ax + by = gcd(a, b) 。
十七、RSA加密演算法。一种加密算法,日后再做详细介绍。
十八、遗传算法。可参考本人写的关于GA 算法的这篇文章:七、遗传算法 透析GA本质。
十九、最大期望(EM)算法。
此算法入选数据挖掘领域十大经典算法。在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;第二步是最大化(M),最大化在 E 步上求得的最大似然值来计算参数的值。M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
二十、数据压缩
数据压缩是通过减少计算机中所存储数据或者通信传播中数据的冗余度,达到增大数据密度,最终使数据的存储空间减少的技术。数据压缩在文件存储和分布式系统领域有着十分广泛的应用。数据压缩也代表着尺寸媒介容量的增大和网络带宽的扩展。
二十一、Hash函数
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。关于hash表的详细阐述,请参考此篇文章:十一、从头到尾彻底解析Hash表算法。
二十二、Dynamic Programming(动态规划)。关于动态规划的粗略介绍,请参考此文:三、dynamic programming。
二十三、堆排序算法。
堆排序算法作为一种快速稳定的算法,其平均时间复杂度(最坏也为)O(n*lgn)。当然,在实际应用中,一个实现的好的快速排序算法仍然要优于堆排序算法。不过,堆数据结构还可以作为高效的优先级队列。对堆排序算法作简单了解,可参考这:堆排序算法。
二十四、递归与回溯算法。此俩个算法,相信各位比较熟悉,在此不做赘述。
二十五、最长公共子序列
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个数列 S ,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
动态规划的一个计算最长公共子序列的方法如下:
以两个序列 X、Y 为例子:
设有二维数组 f[j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度,则有:
f[1][1] = same(1,1)
f[j] = max{f[i-1][j-1]+same(i,j),f[i-1][j],f[j-1]}
其中,same(a,b)当 X 的第 a 位与 Y 的第 b 位完全相同时为“1”,否则为“0”。
此时,f[j]中最大的数便是 X 和 Y 的最长公共子序列的长度,依据该数组回溯,便可找出最长公共子序列。
该算法的空间、时间复杂度均为O(n2),经过优化后,空间复杂度可为O(n),时间复杂度为O(nlogn)。更多详情,参见之前写的一篇拙文(不过,鉴于写的糟,日后会重写):三、dynamic programming。
二十六、红黑树的算法与实现
关于红黑树,linux内核中有实现,本BLOG内也已经写了4篇红黑树系列的文章。详情,请参考:五(续)、教你透彻了解红黑树。
二十七、A*搜寻算法。
相对于BFS、Dijkstra 等算法,A*搜寻算法作为一种高效的最短路径搜索算法,如今,已得到日益广泛的应用。初步了解A*搜寻算法的高效及与其它最短路径算法的比较,请参考此文:一(续)、A*,Dijkstra,BFS算法性能比较及A*算法的应用。
二十八、图像特征提取与匹配之SIFT算法
sift,尺度不变特征转换,是一种电脑视觉的算法用来侦测与描述影像中的局部性特征,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量,此算法由 David Lowe 在1999年所发表,2004年完善总结。关于此算法,请参考如下,粗略介绍:九、图像特征提取与匹配之SIFT算法,利用第三方库编译过程:九(续)、sift算法的编译与实现,c语言一步一步实现sift算法:九之再续:一步一步用c语言实现sift算法、上,及九之再续:教你一步一步用c语言实现sift算法、下。
2012年1月5日星期四
USB转串口完全手册
该方法意味着仅仅需要重新设计嵌入式应用电路板以腾出空间容纳新的元件,但它不用改变固件和PC应用程序。
劣势是却失去了采用USB所带来的大部分好处。实际上,USB能够更快地传输数据,传输速度可达到典型串行端口的100倍(12 Mbps与115 kbps),续使用UART,就会成为主要的设计瓶颈。另外,由于大部分USB-UART接口器件缺乏灵活性,无法实现灵活的电源管理,而这在许多嵌入式设计中是一个关键特性。
此类IC,市场上主要有以下:
未来科技(future technology)
USB-UART的型号如下:
FT232BM/BL/BQ: USB口和串口(UART)的转换。
FT245BM/BL/BQ: 实现USB口和并口(FIFO)的转换
FT2232D: 可以支持USB转两个串口或并口
FT245R: 实现USB口和并口(FIFO)的转换
FT232R: USB口和串口(UART)的转换,同步,异步BIT-BANG接口模式
台湾玖旺科技(prolific)
PL-2303: 低成本USB-UART,USB1.0(1)
PL-2303HX: USB-UART,支持sub 2.0full-speed
PL-2313 USB:USB转双路UART
Silicon Laboratories:
CP2102:USB-UART转换器,实现USB2.0到UART
南京沁恒:
CH432: 双USB-UART
CH341: USB 总线的转接芯片,USB-UART,PARP,同步串行接口。